本篇文章转载自微信公众号“IT成长之家”,IT成长之家出了一个系列的数据分析课程,涉及数据分析、挖掘、预测等等方面的知识。如果大家感兴趣的话可以点击本文下边原文链接到IT成长之家公众号进行学习。
01 前言
线性回归分析是一种很常见的数据分析方法。用于分析因变量是如何受到一个或多个自变量影响的。常用来分析或者预测某个产品的销量与产品的价格、质量、市场活动等等因素之间的关系。
线性回归根据自变量的多少,分为一元线性回归和多元线性回归。当然在实际工作生活中,我们往往都是面对着多元线性回归。
02 案例介绍
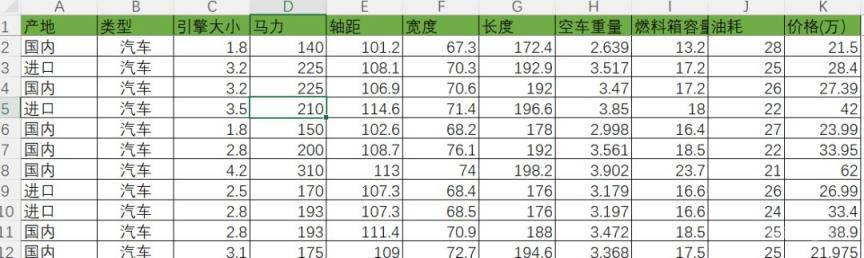
在本案例中,我们有这样的一份数据。已知汽车的产地、类型、型号等等基本属性(A-J列),同时也知道它的价格(K列)。
现在我们需要找出价格(因变量)与这些基本属性(自变量)之间的关系,找出是否存在一个模型(方程),从而来判断新生产的汽车,它对应的价格应该定价在哪比较合适。
03 操作分析
1)打开Excel加载项:文件-选项-加载项-转到,勾上“数据分析库”,点击确定。
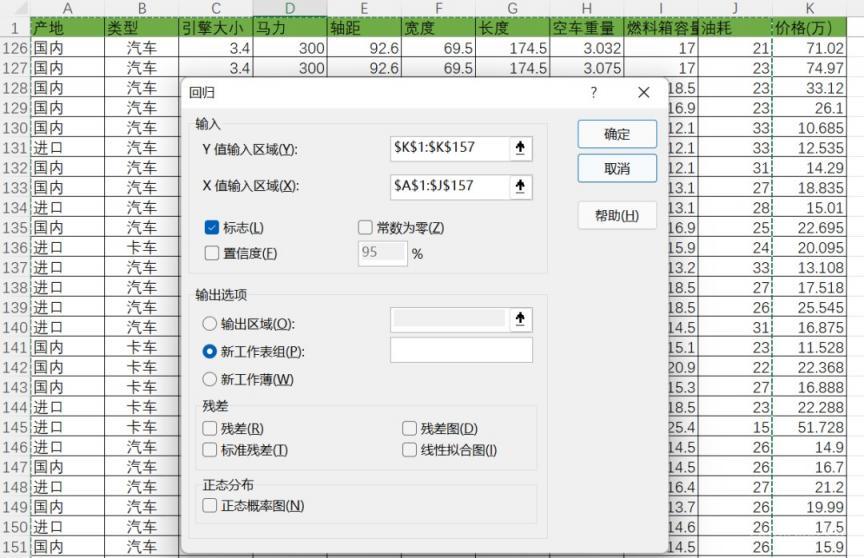
2)点击Excel菜单栏 "数据"- "数据分析", 选择“回归”,Y值区域选择K列范围,X值区域选择所有自变量因素。点击确定。
(注意,在此模型中,我们需要先对“产地”,“类型”进行数值转换,比如0,1代替)
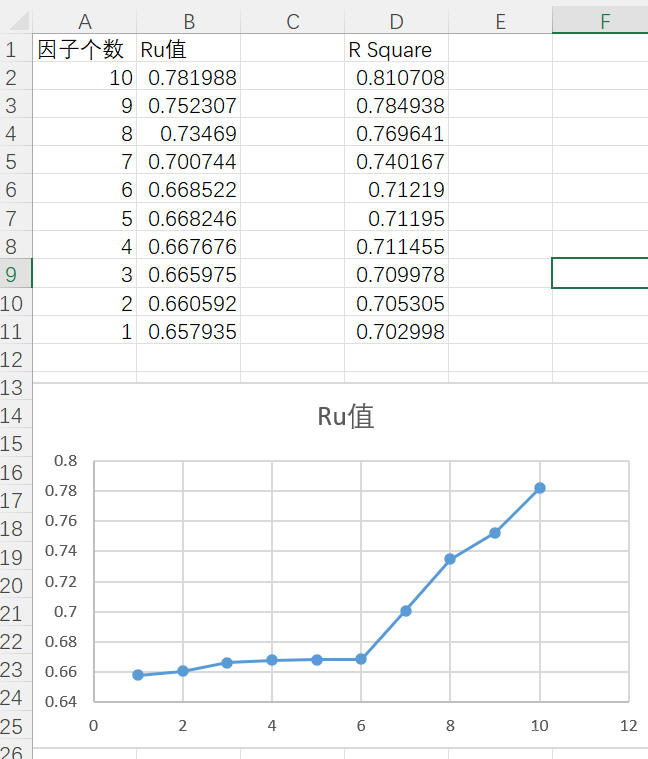
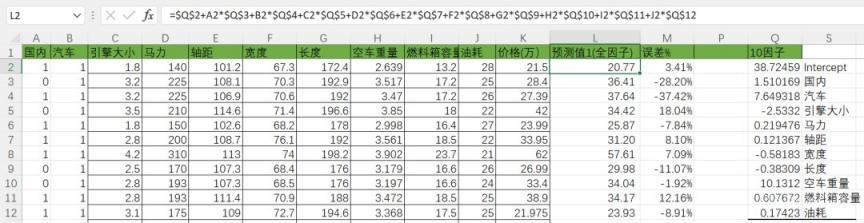
3)回归方程建立之后,我们求出Ru,然后根据t-Stat(影响度)进行排序,去除影响度最低的因子,反复求出Ru值,直到最后一个因子。
4)求出10个Ru值,根据Ru值可以看到,最优的回归方程是Ru值最大的,即10个因子。
5)因此我们的回归方程即可出来(Y= 常量+a*x1+b*x2+....)
同时也可以求出误差率,对预测值的误差有个整体判断。
04 回归方程的解读
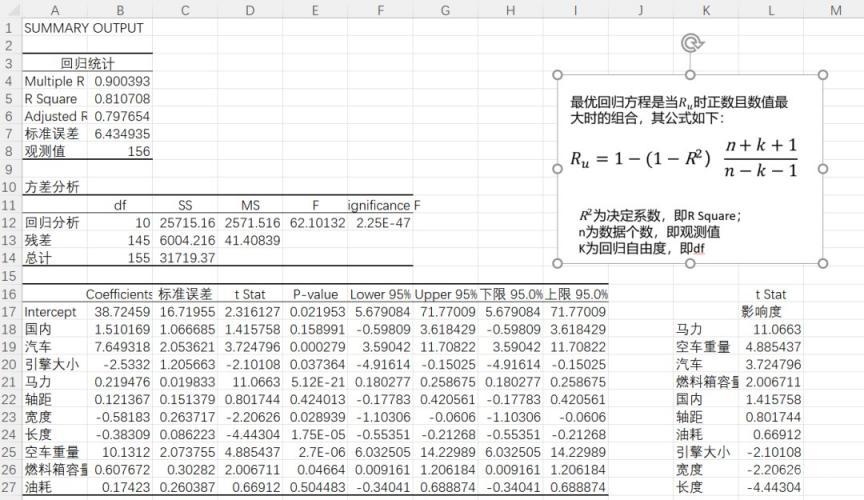
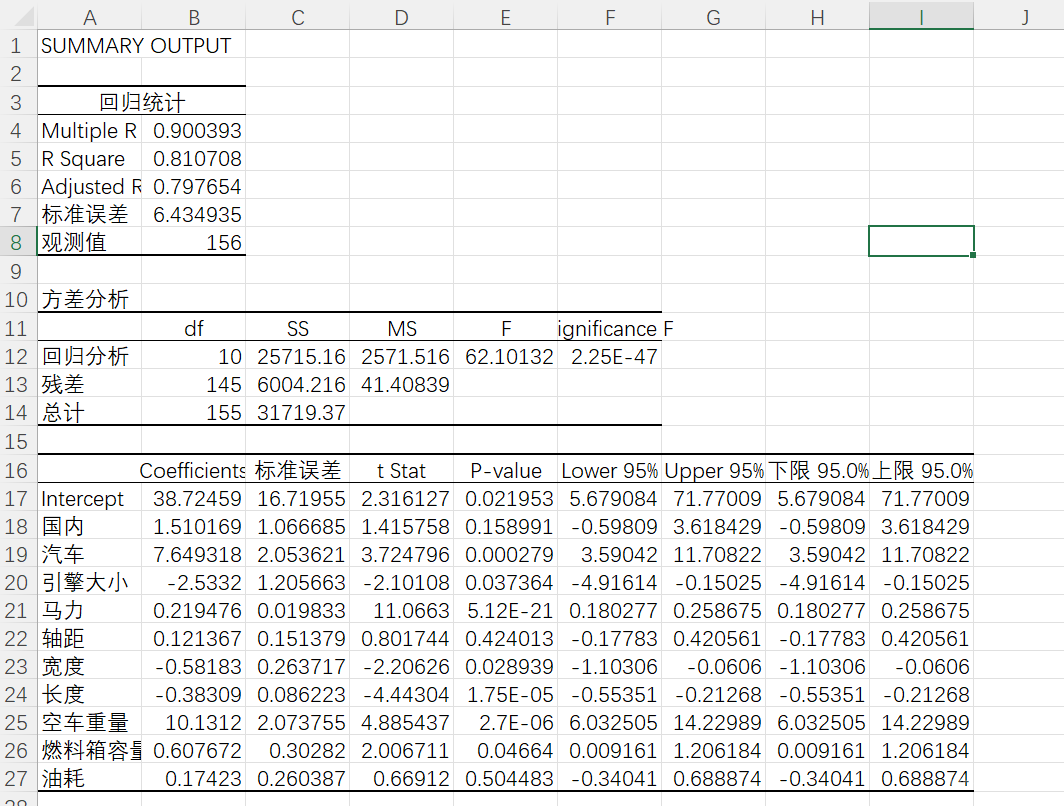
第一个模块为回归统计表,其中主要包含MultipleR、RSquare、AdjustedRSquare、标准误差和观测值。
MultipleR为复相关系数,也就是前面说的相关系数,用来衡量x和y之间的相关程度大小。R Square为复测定系数R2,其用来说明自变量解释因变量变差的程度,从而测量同因变量y的拟合效果。Adjusted R Square为调整后的复测定系数R2,标准误差衡量拟合程度大小,值越小,说明拟合程度越好,观测值指的是用于估计回归方程数据的观测值个数。
例如,从上面结果可以看出,MultipleR为0.900393,表明是有很强的正相关性;R Square为0.810708表明用自变量可解释因变量变差的81.07%;AdjustedRSquare为0.797654,说明自变量能说明因变量的79.76%,因变量剩余的21%则由其他因素来解释。
第二个模块为方差分析表。其主要作用是通过假设检验中的F-检验来判断回归模型的回归效果。
第三个模块是回归参数表。第一列表示截距;第二列表示对应模型的回归系数,包括了截距和斜率,可以根据这个建立回归模型;第三列为回归系数的标准误差,值越小,表明参数的精确度越高;第四列对应的是回归系数/标准误差,对于一元线性回归,F值与t值都与相关系数R代表差不多的意思,但是,对于多元线性回归,t检验是有必要的。第五列为各个回归系数的P值,当P<0.05时,可以认为模型在α=0.05的水平上显著,或置信度达到了95%。最后几列为回归系数置信区间的上限和下限。
05 最后
当然,预测是代表着有一定的不确定性。这些不确定性包括无法解释的原因以及不能预测的波动性。因此预测不可避免的会产生误差。
并且,建立线性回归模型也必须满足一定的条件:例如方差齐性,独立性,正态分布等等。
好了,如果想查看本例使用的数据,请在微信公众号“IT成长之家”后台回复 "线性回归",将会自动发送本推文所用的EXCEL表,包括初始数据、数据处理及模型建立的全过程。下期再会!




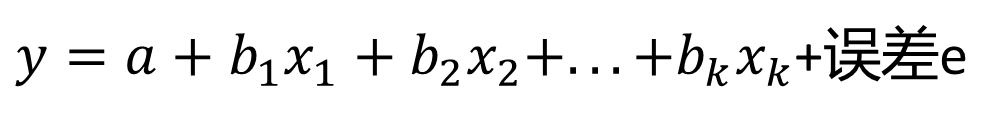







还没有评论,来说两句吧...