回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。通过数据间相关性分析的研究,进一步建立自变量Xi(i=1,2,3,…)与因变量Y之间的回归函数关系,即回归分析模型,从而预测数据的发展趋势。
按照自变量与因变量之间的关系类型,可以分为线性回归与非线性回归。因此我们可以理解为,线性回归只是回归分析所用方法之一,体现出的是变量之间的线性关系。
线性回归的表达式为:Y=b*X+a(a为误差服从均值为0的正态分布)
其中线性回归分析按照涉及自变量的多少,分为一元线性回归分析和多元线性回归分析。
一元线性回归分析
只包括单个自变量和一个因变量,且二者的关系可用一条直线近似表示。它主要研究单个自变量X对因变量Y是否有影响。
比如,身高(X)与体重(Y)的影响。
多元线性回归分析
包括两个或两个以上的自变量,且因变量和自变量之间是线性关系。它主要研究多个自变量X1、X2….Xn对因变量Y是否有影响。
比如,身高(X1)、饮食情况(X2)…运动量(Xn)等因素对体重(Y)的影响。
用Excel研究回归分析的主要问题有四个:
1、确定Y与X间的定量关系表达式,这种表达式称为回归方程;
2、对求得的回归方程的可信度进行检验;
3、判断自变量X对因变量Y有无影响;
4、利用所求得的回归方程进行预测和控制。
1、置信度
95%置信区间指的是某个总体参数的真实值有95%的概率会落在测量结果的区间内。
例如:通过测量某班级学生的考试成绩,得到有95%的置信水平该班成绩的置信区间在60分到80分之间。
那么可以说:在多次抽样后,由95%的样本得到的区间会包含该班学生考试的平均成绩的真值。
置信区间在频率学派中间使用,其在贝叶斯统计中的对应概念是可信区间。两者建立在不同的概念基础上的,贝叶斯统计将分布的位置参数视为随机变量,并对给定观测到的数据之后未知参数的后验分布进行描述。
故无论对随机样本还是已观测数据,构造出来的可信区间,其可信水平都是一个合法的概率;而置信区间的置信水平,只在考虑随机样本时可以被理解为一个概率。
2、R(Multiple R)
回归分析中r值表示相关系数,相关系数r值度量两变量之间的线性相关性。r值取值范围为【-1,+1】。相关系数为-1,表示完全负相关;相关系数为+1,表示完全正相关。相关系数为0表示两变量之间无线性相关性。
3、可决系数(R-squared)
4、调整后的可决系数(Adjusted R Square)
即经自由度修正后的可决系数,从计算公式可知调整后的可决系数小于可决系数,并且可决系数可能为负,此时说明模型极不可靠。
5、P值(P-value)
P值为理论T值超越样本T值的概率,应该联系显著性水平α相比,α表示原假设成立的前提下,理论T值超过样本T值的概率,当P值<α值,说明这种结果实际出现的概率的概率比在原假设成立的前提下这种结果出现的可能性还小但它偏偏出现了,因此拒绝接受原假设。
6、回归方程怎么写
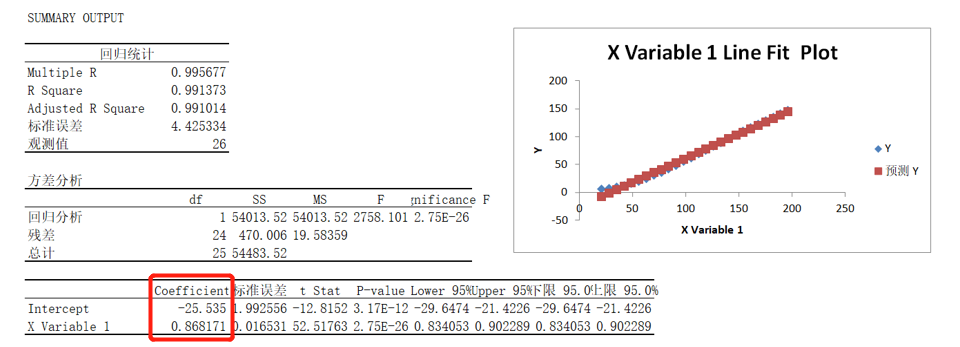
回归方程要根据回归分析的结果中的系数(Coefficients)去写,也分一元线性回归方程和多元线性回归方程。
下面李海博客以一元线性回归方程为例讲一下写法:
根据分析结果中的系数(Coefficients),一元线性回归方程写法为 Y=0.868171X-25.535。
多元线性回归方程写法为 Y=系数1*X1+系数2*X2+系数3*X3-截距(Intercept)。
以上就是李海博客总结的用Excel做回归分析时常见的一些问题,包括置信度,R,R-Square,P,回归方程等。










还没有评论,来说两句吧...